Defines | |
| #define | MAL_MATRIX(name, type) |
| Defines a matrix named name and of type type. | |
| #define | MAL_MATRIX_DIM(name, type, nb_rows, nb_cols) |
| Defines a matrix named name of type type, with size (nb_rows, nb_cols ). It can be use for declaration. | |
| #define | MAL_MATRIX_RESIZE(name, type, nb_rows, nb_cols) |
| Resize the matrix named name to (nb_rows, nb_cols). This acts as a function. | |
| #define | MAL_MATRIX_NB_ROWS(name) |
| Returns the number of rows of matrix name. | |
| #define | MAL_MATRIX_NB_COLS(name) |
| Returns the number of cols of matrix name. | |
| #define | MAL_MATRIX_CLEAR(name) |
| Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function. | |
| #define | MAL_INVERSE(name, inv_matrix, type) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 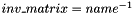 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. | |
| #define | MAL_PSEUDOINVERSE(matrix, pinv_matrix, type) |
Returns in pinv_matrix the pseudo-inverse of matrix name. name can be of arbitrary size. 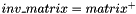 For implementation issue, the type of the data must be specified in type. This macro acts as a function. For implementation issue, the type of the data must be specified in type. This macro acts as a function. | |
| #define | MAL_RET_TRANSPOSE(matrix) |
| Returns the transpose of matrix, i.e. go through a temporary matrix. | |
| #define | MAL_TRANSPOSE_A_in_At(matrix) |
| Puts the transpose of matrix directly inside the argument. | |
| #define | MAL_RET_A_by_B(A, B) |
Returns the product of A by B, i.e. 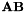 This forces the use of a temporary matrix structure. This forces the use of a temporary matrix structure. | |
| #define | MAL_C_eq_A_by_B(C, A, B) |
Puts in C the result of the product of A by B, i.e. 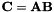 . . | |
| #define | MAL_MATRIX_SET_IDENTITY(matrix) |
| Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero. | |
| #define | MAL_MATRIX_FILL(matrix, value) |
| Fill the matrix named matrix with the value value. | |
| #define | MAL_RET_MATRIX_DATABLOCK(matrix) |
| Returns a pointer on the data stored for the matrix. | |
| #define | MAL_MATRIX_C_eq_EXTRACT_A(C, A, type, top, left, nbrows, nbcols) |
| This is used to extract a submatrix C from A. | |
| #define | MAL_MATRIX_RET_DETERMINANT(name, type) |
| This macro returns the determinant of matrix name. | |
| #define | MAL_VECTOR(name, type) |
| declare a vector named name with type type | |
| #define | MAL_VECTOR_DIM(name, type, nb_rows) |
| declare a vector named name with type type and of size nb_rows | |
| #define | MAL_VECTOR_SIZE(name) |
| returns the size of the vector named name | |
| #define | MAL_VECTOR_RESIZE(name, nb_rows) |
| Resizes of the vector named name . It acts as a function. | |
| #define | MAL_VECTOR_FILL(name, value) |
| Fill the vector named name with the value value. The user is responsible to make sure that the type are compatible. It acts as a function. | |
| #define | MAL_VECTOR_NORM(name) |
Returns the two norms of the vector named name. More precisely if the vector name is of size 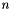 , the norm is defined as: , the norm is defined as: 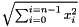 . . | |
| #define | MAL_VECTOR_3D_CROSS_PRODUCT(res, v1, v2) |
Returns in res the cross product of two vectors 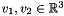 . The cross product . The cross product 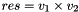 is defined as: is defined as:
| |
| #define | MAL_RET_VECTOR_DATABLOCK(name) |
| Returns a direct access to the data information. It is implementation dependent. However most of the time, it is assume to be an array of data. | |