Defines | |
| #define | MAL_MATRIX(name, type) |
| Defines a matrix named name and of type type. | |
| #define | MAL_MATRIX_DIM(name, type, nb_rows, nb_cols) |
| Defines a matrix named name of type type, with size (nb_rows, nb_cols ). It can be use for declaration. | |
| #define | MAL_MATRIX_RESIZE(name, type, nb_rows, nb_cols) |
| Resize the matrix named name to (nb_rows, nb_cols). This acts as a function. | |
| #define | MAL_MATRIX_NB_ROWS(name) |
| Returns the number of rows of matrix name. | |
| #define | MAL_MATRIX_NB_COLS(name) |
| Returns the number of cols of matrix name. | |
| #define | MAL_MATRIX_CLEAR(name) |
| Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function. | |
| #define | MAL_INVERSE(name, inv_matrix, type) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 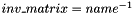 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. | |
| #define | MAL_PSEUDOINVERSE(matrix, pinv_matrix, type) |
Returns in pinv_matrix the pseudo-inverse of matrix name. name can be of arbitrary size. 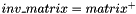 For implementation issue, the type of the data must be specified in type. This macro acts as a function. For implementation issue, the type of the data must be specified in type. This macro acts as a function. | |
| #define | MAL_RET_TRANSPOSE(matrix) |
| Returns the transpose of matrix, i.e. go through a temporary matrix. | |
| #define | MAL_TRANSPOSE_A_in_At(matrix) |
| Puts the transpose of matrix directly inside the argument. | |
| #define | MAL_RET_A_by_B(A, B) |
Returns the product of A by B, i.e. 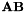 This forces the use of a temporary matrix structure. This forces the use of a temporary matrix structure. | |
| #define | MAL_C_eq_A_by_B(C, A, B) |
Puts in C the result of the product of A by B, i.e. 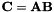 . . | |
| #define | MAL_MATRIX_SET_IDENTITY(matrix) |
| Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero. | |
| #define | MAL_MATRIX_FILL(matrix, value) |
| Fill the matrix named matrix with the value value. | |
| #define | MAL_RET_MATRIX_DATABLOCK(matrix) |
| Returns a pointer on the data stored for the matrix. | |
| #define | MAL_MATRIX_C_eq_EXTRACT_A(C, A, type, top, left, nbrows, nbcols) |
| This is used to extract a submatrix C from A. | |
| #define | MAL_MATRIX_RET_DETERMINANT(name, type) |
| This macro returns the determinant of matrix name. | |
| #define | MAL_S3x3_MATRIX(name, type) |
| Defines a matrix named name and of type type. | |
| #define | MAL_S3x3_MATRIX_CLEAR(name) |
| Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function. | |
| #define | MAL_S3x3_INVERSE(name, inv_matrix, type) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 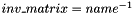 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. | |
| #define | MAL_S3x3_RET_TRANSPOSE(matrix) |
| Returns the transpose of matrix. | |
| #define | MAL_S3x3_RET_A_by_B(A, B) |
Returns the product of A by B, i.e. 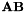 This forces the use of a temporary matrix structure. This forces the use of a temporary matrix structure. | |
| #define | MAL_S3x3_C_eq_A_by_B(C, A, B) |
Puts in C the result of the product of A by B, i.e. 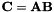 . . | |
| #define | MAL_S3x3_MATRIX_SET_IDENTITY(matrix) |
| Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero. | |
| #define | MAL_S3x3_MATRIX_FILL(matrix, value) |
| Fill the matrix named matrix with the value value. | |
| #define | MAL_S3x3_RET_MATRIX_DATABLOCK(matrix) |
| Returns a pointer on the data stored for the matrix. | |
| #define | MAL_S3x3_MATRIX_C_eq_EXTRACT_A(C, A, type, top, left, nbrows, nbcols) |
| This is used to extract a submatrix C from A. | |
| #define | MAL_S3x3_MATRIX_RET_DETERMINANT(name, type) |
| This macro returns the determinant of matrix name. | |
| #define | MAL_S3x3_MATRIX_ACCESS_I(name, i) |
| This macro returns the element at position i name(i) | |
| #define | MAL_S3x3_MATRIX_ACCESS_I_J(name, i, j) |
| This macro returns element at pos (i,j) | |
| #define | MAL_S4x4_MATRIX(name, type) |
| Defines a matrix named name and of type type. | |
| #define | MAL_S4x4_MATRIX_CLEAR(name) |
| Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function. | |
| #define | MAL_S4x4_INVERSE(name, inv_matrix, type) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 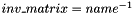 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function. | |
| #define | MAL_S4x4_RET_TRANSPOSE(matrix) |
| Returns the transpose of matrix. | |
| #define | MAL_S4x4_RET_A_by_B(A, B) |
Returns the product of A by B, i.e. 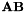 This forces the use of a temporary matrix structure. This forces the use of a temporary matrix structure. | |
| #define | MAL_S4x4_C_eq_A_by_B(C, A, B) |
Puts in C the result of the product of A by B, i.e. 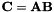 . . | |
| #define | MAL_S4x4_MATRIX_SET_IDENTITY(matrix) |
| Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero. | |
| #define | MAL_S4x4_MATRIX_FILL(matrix, value) |
| Fill the matrix named matrix with the value value. | |
| #define | MAL_S4x4_RET_MATRIX_DATABLOCK(matrix) |
| Returns a pointer on the data stored for the matrix. | |
| #define | MAL_S4x4_MATRIX_C_eq_EXTRACT_A(C, A, type, top, left, nbrows, nbcols) |
| This is used to extract a submatrix C from A. | |
| #define | MAL_S4x4_MATRIX_RET_DETERMINANT(name, type) |
| This macro returns the determinant of matrix name. | |
| #define | MAL_S4x4_MATRIX_ACCESS_I(name, i) |
| This macro returns the element at position i name(i) | |
| #define | MAL_S4x4_MATRIX_ACCESS_I_J(name, i, j) |
| This macro returns element at pos (i,j) | |
| #define MAL_C_eq_A_by_B | ( | C, | |
| A, | |||
| B | |||
| ) |
Puts in C the result of the product of A by B, i.e. 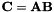 .
.
Example
MAL_MATRIX(A,double); MAL_MATRIX(B,double); MAL_MATRIX(C,double); ... MAL_C_eq_A_by_B(C,A,B);
This notation should be used to avoid temporary matrix, and should be avoided when writting something like:
MAL_MATRIX(A,double); MAL_MATRIX(B,double); ... MAL_C_eq_A_by_B(A,A,B);
instead you should write:
A = MAL_RET_A_by_B(A,B);
| #define MAL_INVERSE | ( | name, | |
| inv_matrix, | |||
| type | |||
| ) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 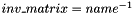 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
Example:
MAL_MATRIX(A,5,5,double); MAL_MATRIX(pA,5,5,double); ... MAL_INVERSE(A,iA,double);
| #define MAL_MATRIX | ( | name, | |
| type | |||
| ) |
Defines a matrix named name and of type type.
| #define MAL_MATRIX_C_eq_EXTRACT_A | ( | C, | |
| A, | |||
| type, | |||
| top, | |||
| left, | |||
| nbrows, | |||
| nbcols | |||
| ) |
This is used to extract a submatrix C from A.
For implementation purposes the data type is specified by type. The submatrix extracted is specified by its top - left coordinates, and its size: nbrows and nbcols for the number of rows and columns respectivly.
| #define MAL_MATRIX_CLEAR | ( | name | ) |
Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function.
| #define MAL_MATRIX_DIM | ( | name, | |
| type, | |||
| nb_rows, | |||
| nb_cols | |||
| ) |
Defines a matrix named name of type type, with size (nb_rows, nb_cols ). It can be use for declaration.
| #define MAL_MATRIX_FILL | ( | matrix, | |
| value | |||
| ) |
Fill the matrix named matrix with the value value.
Example:
MAL_MATRIX(A,3,3); ... MAL_MATRIX_FILL(A,0);
| #define MAL_MATRIX_NB_COLS | ( | name | ) |
Returns the number of cols of matrix name.
| #define MAL_MATRIX_NB_ROWS | ( | name | ) |
Returns the number of rows of matrix name.
| #define MAL_MATRIX_RESIZE | ( | name, | |
| type, | |||
| nb_rows, | |||
| nb_cols | |||
| ) |
Resize the matrix named name to (nb_rows, nb_cols). This acts as a function.
| #define MAL_MATRIX_RET_DETERMINANT | ( | name, | |
| type | |||
| ) |
This macro returns the determinant of matrix name.
For implementation purposes the type has to be specified by type.
| #define MAL_MATRIX_SET_IDENTITY | ( | matrix | ) |
Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero.
if

then with
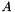 becomes
becomes
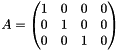
| #define MAL_PSEUDOINVERSE | ( | matrix, | |
| pinv_matrix, | |||
| type | |||
| ) |
Returns in pinv_matrix the pseudo-inverse of matrix name. name can be of arbitrary size. 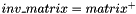 For implementation issue, the type of the data must be specified in type. This macro acts as a function.
For implementation issue, the type of the data must be specified in type. This macro acts as a function.
Example:
MAL_MATRIX(A,double); MAL_MATRIX(pA,double); ... MAL_PSEUDOINVERSE(A,pA,double);
| #define MAL_RET_A_by_B | ( | A, | |
| B | |||
| ) |
Returns the product of A by B, i.e. 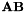 This forces the use of a temporary matrix structure.
This forces the use of a temporary matrix structure.
Example:
MAT_MATRIX(A,double); MAT_MATRIX(B,double); MAL_MATRIX(C,double); ... C = MAL_RET_A_by_B(A,B);
| #define MAL_RET_MATRIX_DATABLOCK | ( | matrix | ) |
Returns a pointer on the data stored for the matrix.
This is specially useful for mapping with fortran routines, for instance LAPACK.
| #define MAL_RET_TRANSPOSE | ( | matrix | ) |
Returns the transpose of matrix, i.e. go through a temporary matrix.
Example:
MAL_MATRIX(A,double); MAL_MATRIX(At,double); ... At = MAL_TRANSPOSE(A);
| #define MAL_S3x3_C_eq_A_by_B | ( | C, | |
| A, | |||
| B | |||
| ) |
Puts in C the result of the product of A by B, i.e. 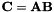 .
.
Example
MAL_S3x3_MATRIX(A,double); MAL_S3x3_MATRIX(B,double); MAL_S3x3_MATRIX(C,double); ... MAL_S3x3_C_eq_A_by_B(C,A,B);
This notation should be used to avoid temporary matrix, and should be avoided when writting something like:
MAL_S3x3_MATRIX(A,double); MAL_S3x3_MATRIX(B,double); ... MAL_S3x3_C_eq_A_by_B(A,A,B);
instead you should write:
A = MAL_S3x3_RET_A_by_B(A,B);
| #define MAL_S3x3_INVERSE | ( | name, | |
| inv_matrix, | |||
| type | |||
| ) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 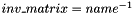 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
Example:
MAL_S3x3_MATRIX(A,5,5,double); MAL_S3x3_MATRIX(pA,5,5,double); ... MAL_S3x3_INVERSE(A,iA,double);
| #define MAL_S3x3_MATRIX | ( | name, | |
| type | |||
| ) |
Defines a matrix named name and of type type.
| #define MAL_S3x3_MATRIX_ACCESS_I | ( | name, | |
| i | |||
| ) |
This macro returns the element at position i name(i)
| #define MAL_S3x3_MATRIX_ACCESS_I_J | ( | name, | |
| i, | |||
| j | |||
| ) |
This macro returns element at pos (i,j)
name(i,j)
| #define MAL_S3x3_MATRIX_C_eq_EXTRACT_A | ( | C, | |
| A, | |||
| type, | |||
| top, | |||
| left, | |||
| nbrows, | |||
| nbcols | |||
| ) |
This is used to extract a submatrix C from A.
For implementation purposes the data type is specified by type. The submatrix extracted is specified by its top - left coordinates, and its size: nbrows and nbcols for the number of rows and columns respectivly.
| #define MAL_S3x3_MATRIX_CLEAR | ( | name | ) |
Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function.
| #define MAL_S3x3_MATRIX_FILL | ( | matrix, | |
| value | |||
| ) |
Fill the matrix named matrix with the value value.
Example:
MAL_S3x3_MATRIX(A,3,3); ... MAL_S3x3_MATRIX_FILL(A,0);
| #define MAL_S3x3_MATRIX_RET_DETERMINANT | ( | name, | |
| type | |||
| ) |
This macro returns the determinant of matrix name.
For implementation purposes the type has to be specified by type.
| #define MAL_S3x3_MATRIX_SET_IDENTITY | ( | matrix | ) |
Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero.
if

then with
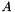 becomes
becomes
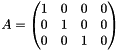
| #define MAL_S3x3_RET_A_by_B | ( | A, | |
| B | |||
| ) |
Returns the product of A by B, i.e. 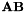 This forces the use of a temporary matrix structure.
This forces the use of a temporary matrix structure.
Example:
MAL_S3x3_MATRIX(A,double); MAL_S3x3_MATRIX(B,double); MAL_S3x3_MATRIX(C,double); ... C = MAL_S3x3_RET_A_by_B(A,B);
| #define MAL_S3x3_RET_MATRIX_DATABLOCK | ( | matrix | ) |
Returns a pointer on the data stored for the matrix.
This is specially useful for mapping with fortran routines, for instance LAPACK.
| #define MAL_S3x3_RET_TRANSPOSE | ( | matrix | ) |
Returns the transpose of matrix.
Example:
MAL_S3x3_MATRIX(A,double); MAL_S3x3_MATRIX(At,double); ... At = MAL_S3x3_TRANSPOSE(A);
| #define MAL_S4x4_C_eq_A_by_B | ( | C, | |
| A, | |||
| B | |||
| ) |
Puts in C the result of the product of A by B, i.e. 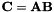 .
.
Example
MAL_S4x4_MATRIX(A,double); MAL_S4x4_MATRIX(B,double); MAL_S4x4_MATRIX(C,double); ... MAL_S4x4_C_eq_A_by_B(C,A,B);
This notation should be used to avoid temporary matrix, and should be avoided when writting something like:
MAL_S4x4_MATRIX(A,double); MAL_S4x4_MATRIX(B,double); ... MAL_S4x4_C_eq_A_by_B(A,A,B);
instead you should write:
A = MAL_S4x4_RET_A_by_B(A,B);
| #define MAL_S4x4_INVERSE | ( | name, | |
| inv_matrix, | |||
| type | |||
| ) |
Returns in inv_matrix, the inverse of matrix name. name should be a square matrix. 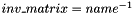 For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
For implementation issue, the type of the data must be specified in type. You should read the documentation of the specific implementation to handle properly the numerical issues. This macro acts as a function.
Example:
MAL_S4x4_MATRIX(A,5,5,double); MAL_S4x4_MATRIX(pA,5,5,double); ... MAL_S4x4_INVERSE(A,iA,double);
| #define MAL_S4x4_MATRIX | ( | name, | |
| type | |||
| ) |
Defines a matrix named name and of type type.
| #define MAL_S4x4_MATRIX_ACCESS_I | ( | name, | |
| i | |||
| ) |
This macro returns the element at position i name(i)
| #define MAL_S4x4_MATRIX_ACCESS_I_J | ( | name, | |
| i, | |||
| j | |||
| ) |
This macro returns element at pos (i,j)
name(i,j)
| #define MAL_S4x4_MATRIX_C_eq_EXTRACT_A | ( | C, | |
| A, | |||
| type, | |||
| top, | |||
| left, | |||
| nbrows, | |||
| nbcols | |||
| ) |
This is used to extract a submatrix C from A.
For implementation purposes the data type is specified by type. The submatrix extracted is specified by its top - left coordinates, and its size: nbrows and nbcols for the number of rows and columns respectivly.
| #define MAL_S4x4_MATRIX_CLEAR | ( | name | ) |
Clear the matrix name , i.e. put all the value to 0. In some case, it also mean that the data is deallocated. It is wise to resize the matrix after the call to this macro. This macro acts as a function.
| #define MAL_S4x4_MATRIX_FILL | ( | matrix, | |
| value | |||
| ) |
Fill the matrix named matrix with the value value.
Example:
MAL_S4x4_MATRIX(A,3,3); ... MAL_S4x4_MATRIX_FILL(A,0);
| #define MAL_S4x4_MATRIX_RET_DETERMINANT | ( | name, | |
| type | |||
| ) |
This macro returns the determinant of matrix name.
For implementation purposes the type has to be specified by type.
| #define MAL_S4x4_MATRIX_SET_IDENTITY | ( | matrix | ) |
Set the matrix named matrix to the identity matrix. When matrix is not square, the identity matrix is set to the upper left greatest square matrix included into matrix. The other values are set to zero.
if

then with
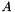 becomes
becomes
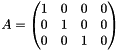
| #define MAL_S4x4_RET_A_by_B | ( | A, | |
| B | |||
| ) |
Returns the product of A by B, i.e. 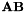 This forces the use of a temporary matrix structure.
This forces the use of a temporary matrix structure.
Example:
MAL_S4x4_MATRIX(A,double); MAL_S4x4_MATRIX(B,double); MAL_S4x4_MATRIX(C,double); ... C = MAL_S4x4_RET_A_by_B(A,B);
| #define MAL_S4x4_RET_MATRIX_DATABLOCK | ( | matrix | ) |
Returns a pointer on the data stored for the matrix.
This is specially useful for mapping with fortran routines, for instance LAPACK.
| #define MAL_S4x4_RET_TRANSPOSE | ( | matrix | ) |
Returns the transpose of matrix.
Example:
MAL_S4x4_MATRIX(A,double); MAL_S4x4_MATRIX(At,double); ... At = MAL_S4x4_TRANSPOSE(A);
| #define MAL_TRANSPOSE_A_in_At | ( | matrix | ) |
Puts the transpose of matrix directly inside the argument.
Example:
MAL_MATRIX(A,double); MAL_MATRIX(At,double); ... MAL_TRANSPOSE_A_in_At(A,At);