First you need to include the header file:

#include "PreviewControl/OptimalControllerSolver.hh"

In the following we will use a pointer towards an instance of class OptimalControllerSolver.

int main()
{
  PatternGeneratorJRL::OptimalControllerSolver *anOCS;

You have then to build the linear discrete system of the linear inverted pendulum such that:

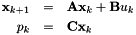
$\begin{eqnarray*} {\bf x}_{k+1} &=& {\bf A}{\bf x}_k + {\bf B} u_{k} \\ p_k &=& {\bf C} {\bf x}_{k} \\ \end{eqnarray*}$

For this we need to declare the associated matrices:

  /* Declare the linear system */
  MAL_MATRIX_DIM(A,double,3,3);
  MAL_MATRIX_DIM(b,double,3,1);
  MAL_MATRIX_DIM(c,double,1,3);
  MAL_MATRIX_TYPE( double) lF;

and the weights of the function to be minimized:

  double Q, R;
  int Nl;
  double T = 0.005;

Then we have to initialize the discretized linear system with

$\begin{eqnarray*} {\bf A} & \equiv & \left[ \begin{matrix} 1 & T & T^2/2 \\ 0 & 1 & T \\ 0 & 0 & 1 \end{matrix} \right] \\ {\bf B} & \equiv & \left[ \begin{matrix} T^3/6 \\ T^2/2 \\ T \end{matrix} \right] \\ {\bf C} & \equiv & \left[ 1 \; 0 \; \frac{-z_c}{g} \right] \end{eqnarray*}$

  /* Build the initial discrete system
     regarding the CoM and the ZMP. */
  A(0,0) = 1.0; A(0,1) =   T; A(0,2) = T*T/2.0;
  A(1,0) = 0.0; A(1,1) = 1.0; A(1,2) = T;
  A(2,0) = 0.0; A(2,1) = 0.0; A(2,2) = 1;

  b(0,0) = T*T*T/6.0;
  b(1,0) = T*T/2.0;
  b(2,0) = T;

  c(0,0) = 1.0;
  c(0,1) = 0.0;
  c(0,2) = -0.814/9.8;

We then have to initialize the weights of the index function:

$J = \sum^{NL}_{j=1} \{ Q(p^{ref}_j -p_j)^2 + Ru_j^2 \}$

  Q = 1.0;
  R = 1e-6;

  Nl = (int)(1.6/T);

To suppress the problem of the initial CoM position, we can reformulate the discrete problem by posing the following:

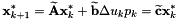
$\begin{eqnarray*} {\bf x}^*_{k+1} = \widetilde{\bf A} {\bf x}^*_{k} + \widetilde{\bf b}\Delta u_k p_k = \widetilde{\bf c}{\bf x}^*_{k} \end{eqnarray*}$

with {eqnarray* u_k u_k - u_{k-1} & { x}_k { x}_k - { x}_{k-1} { x}_k [ {matrix} p_k\ { x}_k {matrix} ] }

$\begin{eqnarray*} \widetilde{\bf A} &\equiv & \left[ \begin{matrix} 1 & {\bf cA} \\ {\bf 0} & {\bf A} \\ \end{matrix} \right] \\ \tilde{\bf b} & \equiv & \left[ \begin{matrix} {\bf cb} \\ {\bf c} \end{matrix} \right] \\ \tilde{\bf c} & \equiv & [ 1 \; 0 \; 0 \; 0] \\ \end{eqnarray*}$

Then the subsequent code performs this operation and displays the associated matrices:

  // Build the derivated system
  MAL_MATRIX_DIM(Ax,double,4,4);
  MAL_MATRIX(tmpA,double);
  MAL_MATRIX_DIM(bx,double,4,1);
  MAL_MATRIX(tmpb,double);
  MAL_MATRIX_DIM(cx,double,1,4);
  
  tmpA = MAL_RET_A_by_B(c,A);
  cout << "tmpA :" << tmpA<<endl;

  Ax(0,0)= 1.0;
  for(int i=0;i<3;i++)
    {
      Ax(0,i+1) = tmpA(0,i);
    Ax(i+1,0) = 0.;
      for(int j=0;j<3;j++)
  Ax(i+1,j+1) = A(i,j);
    }
  cout << "Ax: " << endl << Ax<< endl;

  tmpb = MAL_RET_A_by_B(c,b);
  bx(0,0) = tmpb(0,0);
  for(int i=0;i<3;i++)
    {
      bx(i+1,0) = b(i,0);
    }

  cout << "bx: " << endl << bx << endl;

  cx(0,0) =1.0;   
  cx(0,1) =0.0;
  cx(0,2) =0.0;
  cx(0,3) =0.0;
  cout << "cx: " << endl << cx << endl;

To create the instance of the object solving the Riccati Equation:

  anOCS = new PatternGeneratorJRL::OptimalControllerSolver(Ax,bx,cx,Q,R,Nl);

The computation of the weights is done by calling ComputeWeights(). There is only one parameter to specify, but it is important as the weights are computed differently according to this parameter. If you use the mode without initial position please uses MODE_WITH_INITIALPOS.

  anOCS->ComputeWeights(PatternGeneratorJRL::OptimalControllerSolver::MODE_WITHOUT_INITIALPOS);

To display the weights in the standard output

  anOCS->DisplayWeights();

It is possible to retrieve the weights in a vector:

  anOCS->GetF(lF);

To compute the same weight with a specific initial position and the original linear system you can use :

  anOCS = new PatternGeneratorJRL::OptimalControllerSolver(A,b,c,Q,R,Nl);

  anOCS->ComputeWeights(PatternGeneratorJRL::OptimalControllerSolver::MODE_WITH_INITIALPOS);