This class computes the gains for preview control for a given discrete system. The discrete system is defined by three matrix A, b, c such as :
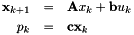
. More...
#include <PreviewControl/OptimalControllerSolver.hh>
Public Member Functions | |
| OptimalControllerSolver (MAL_MATRIX(&A, double), MAL_MATRIX(&b, double), MAL_MATRIX(&c, double), double Q, double R, unsigned int Nl) | |
| ~OptimalControllerSolver () | |
| void | ComputeWeights (unsigned int Mode) |
| void | DisplayWeights () |
| bool | GeneralizedSchur (MAL_MATRIX(&A, double), MAL_MATRIX(&B, double), MAL_VECTOR(&alphar, double), MAL_VECTOR(&alphai, double), MAL_VECTOR(&beta, double), MAL_MATRIX(&L, double), MAL_MATRIX(&R, double)) |
| void | GetF (MAL_MATRIX(&LF, double)) |
| void | GetK (MAL_MATRIX(&LK, double)) |
Static Public Attributes | |
| static const unsigned int | MODE_WITHOUT_INITIALPOS = 1 |
| static const unsigned int | MODE_WITH_INITIALPOS = 0 |
Protected Member Functions | |
| MAL_MATRIX (m_A, double) | |
| MAL_MATRIX (m_b, double) | |
| MAL_MATRIX (m_c, double) | |
| MAL_MATRIX (m_K, double) | |
| MAL_MATRIX (m_F, double) | |
Protected Attributes | |
| double | m_Q |
| double | m_R |
| int | m_Nl |
This class computes the gains for preview control for a given discrete system. The discrete system is defined by three matrix A, b, c such as :
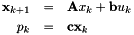
.
The optimal critera considered here is :
![\[ J = \sum^{\infty}_{j=1} \{ Q(p^{ref}_j -p_j)^2 + Ru_j^2 \} \]](form_6.png)
where 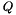 and
and 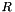 are also given as inputs.
are also given as inputs.
the solution is then:
![\begin{eqnarray*} u_j = - {\bf K}x_k + [ f_1, f_2, \cdots, f_N] \left[ \begin{matrix} p^{ref}_{k+1} \\ \vdots \\ p^{ref}_{k+N} \end{matrix} \right] \end{eqnarray*}](form_9.png)
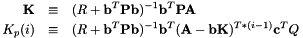
where 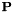 is solution of the following Riccati equation:
is solution of the following Riccati equation:
![\[ {\bf P} = {\bf A}^T {\bf PA} + {\bf c}^TQ{\bf c} - {\bf A}^T{\bf Pb}(R + {\bf b}^T{\bf Pb})^{-1}{\bf b}^T{\bf PA} \]](form_12.png)
The resolution of the Riccati equation is taken from Laub1979, and is based on a Schur form .
To suppress the problem of the initial CoM position, we can reformulate the discrete problem by posing the following:
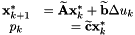
with
![\begin{eqnarray*} \Delta u_k \equiv u_k - u_{k-1} & \Delta {\bf x}_k \equiv {\bf x}_k - {\bf x}_{k-1}\\ {\bf x}_k \equiv \left[ \begin{matrix} p_k\\ \Delta {\bf x}_k \end{matrix} \right] \end{eqnarray*}](form_14.png)
The augmented system is then
![\begin{eqnarray*} \widetilde{\bf A} &\equiv & \left[ \begin{matrix} 1 & {\bf cA} \\ {\bf 0} & {\bf A} \\ \end{matrix} \right] \\ \tilde{\bf b} & \equiv & \left[ \begin{matrix} {\bf cb} \\ {\bf c} \end{matrix} \right] \\ \tilde{\bf c} & \equiv & [ 1 \; 0 \; 0 \; 0] \\ \end{eqnarray*}](form_15.png)
with the following cost function:
![\[ J = \sum^{\infty}_{j=1} \{ Q(p^{ref}_j -p_j)^2 + R \Delta u_j^2 \} \]](form_16.png)
the solution is then:
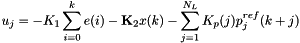
where
![\begin{eqnarray*} \left[ \begin{matrix} K_1 \\ {\bf K}_2 \\ \end{matrix} \right]= \widetilde{\bf K} \end{eqnarray*}](form_18.png)
Alan J. Laub A Schur method for solving Algebraic Riccati Equations, IEEE Transaction on Automatic Control, Vol AC-24, No.6 December 1979
| OptimalControllerSolver::OptimalControllerSolver | ( | MAL_MATRIX &, | double, |
| MAL_MATRIX &, | double, | ||
| MAL_MATRIX &, | double, | ||
| double | Q, | ||
| double | R, | ||
| unsigned int | Nl | ||
| ) |
A constructor
References b, c, MAL_MATRIX, MAL_MATRIX_NB_COLS, MAL_MATRIX_NB_ROWS, and MAL_MATRIX_RESIZE.
Destructor.
| void OptimalControllerSolver::ComputeWeights | ( | unsigned int | Mode | ) |
Compute the weights Following the mode, there is a the inclusion of the P matrix inside the weights.
References MAL_INVERSE, MAL_MATRIX, MAL_MATRIX_DIM, MAL_MATRIX_NB_COLS, MAL_MATRIX_NB_ROWS, MAL_MATRIX_RESIZE, MAL_MATRIX_SET_IDENTITY, MAL_RET_A_by_B, MAL_RET_TRANSPOSE, MAL_VECTOR_DIM, and n.
Referenced by PatternGeneratorJRL::PreviewControl::ComputeOptimalWeights().
Display the weights
| bool OptimalControllerSolver::GeneralizedSchur | ( | MAL_MATRIX &, | double, |
| MAL_MATRIX &, | double, | ||
| MAL_VECTOR &, | double, | ||
| MAL_VECTOR &, | double, | ||
| MAL_VECTOR &, | double, | ||
| MAL_MATRIX &, | double, | ||
| MAL_MATRIX &, | double | ||
| ) |
| void OptimalControllerSolver::GetF | ( | MAL_MATRIX &, | double | ) |
To take matrix F aka the weights of the preview window .
References MAL_MATRIX.
Referenced by PatternGeneratorJRL::PreviewControl::ComputeOptimalWeights().
| void OptimalControllerSolver::GetK | ( | MAL_MATRIX &, | double | ) |
To take matrix K, aka the weight of the other part of the command
References MAL_MATRIX.
Referenced by PatternGeneratorJRL::PreviewControl::ComputeOptimalWeights().
| PatternGeneratorJRL::OptimalControllerSolver::MAL_MATRIX | ( | m_A | , |
| double | |||
| ) | [protected] |
The matrices needed for the dynamical system such as
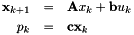
| PatternGeneratorJRL::OptimalControllerSolver::MAL_MATRIX | ( | m_b | , |
| double | |||
| ) | [protected] |
| PatternGeneratorJRL::OptimalControllerSolver::MAL_MATRIX | ( | m_c | , |
| double | |||
| ) | [protected] |
| PatternGeneratorJRL::OptimalControllerSolver::MAL_MATRIX | ( | m_K | , |
| double | |||
| ) | [protected] |
The weights themselves
| PatternGeneratorJRL::OptimalControllerSolver::MAL_MATRIX | ( | m_F | , |
| double | |||
| ) | [protected] |
int PatternGeneratorJRL::OptimalControllerSolver::m_Nl [protected] |
The size of the window for the preview
double PatternGeneratorJRL::OptimalControllerSolver::m_Q [protected] |
The coefficent of the index criteria:
![\[ J = \sum^{\infty}_{j=1} \{ Q(p^{ref}_j -p_j)^2 + Ru_j^2 \} \]](form_6.png)
double PatternGeneratorJRL::OptimalControllerSolver::m_R [protected] |
const unsigned int PatternGeneratorJRL::OptimalControllerSolver::MODE_WITH_INITIALPOS = 0 [static] |
const unsigned int PatternGeneratorJRL::OptimalControllerSolver::MODE_WITHOUT_INITIALPOS = 1 [static] |